
1. 최장 증가 부분 수열
- 원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고,
그 길이가 최대인 부분 수열 - 부분 수열 : 어떤 수열이 주어질 떄, 그 수열에서 일부 원소를 뽑아내어 새로 만든 수열의 부분 수열
- 증가 부분 수열 : 부분수열이 오름차순을 유지하는 것
- LIS : 어떤 수열에서 만들 수 있는 부분 수열 중 가장 길면서 오름차순을 유지하는 수열
- 예시)

위와 같은 길이가 8인 수열이 주어진다고 가정
이 수열에서 증가하는 부분 수열을 뽑는다면 다음과 같이 여러 수열이 나올 것
[2, 3], [1, 3], [2, 5],[2, 3, 5],[1, 3, 5]등등 ▶ 이중 가장 긴 수열은 [2, 3, 5, 6, 7]

물론 [1, 3, 5, 6, 7]도 가장 길이가 긴 수열로 가능함
이와같이, LIS는 반드시 하나가 아닐 수 있음
→ 문제에서도 답으로 LIS의 길이를 출력하도록 하거나, 수열을 구한다면 답이 여러개가 되도록 출제함
2. LIS를 구하는 방법
2-1. DP(Dynamic Programing) 이용 : O(N^2)
- i번째원소를 i-1번쨰 원소와 비교했을때
0~ i-1번째 원소들 중에서 i번쨰 원소보다 작은 원소들의 dp값 중 가장 큰 값을 +1을 db[i]로 기록 - 장점 : 구현이 쉬움
- 단점 : N이 커질 수록 효율이 떨어짐

▶ 시작은 1로시작

▶현재 값은 6이고 6보다 작은 이전 원소들 중 가장 큰 dp값이 1이므로 1+1=2를 현재 dp값으로 기록

▶ 현재값은 3이고 작은 이전 원소들 중에 가장 큰 dp값이 1이므로 1+1=2를 현재 dp값으로 기록

▶ 현재 값은 4고 4보다 작은 이전 원소들 중 가장 큰 dp값이 2이므로 2+1=3을 현재 dp값으로 기록
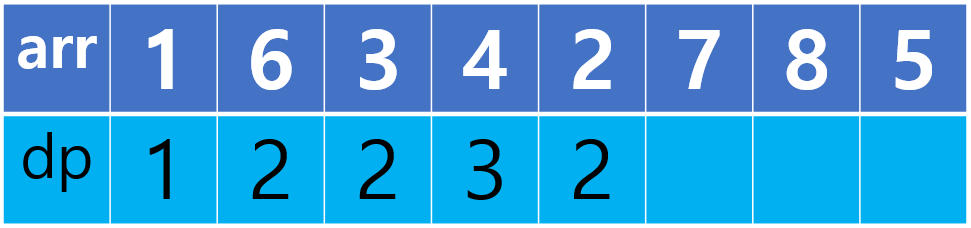
▶ 현재값은 2이고 2보다 작은 이전 원소들 중 가장 큰 dp값이 1이므로 1+1=2를 현재 dp값으로 기록

▶ 현재 값은 7이고 7보다 작은 이전 원소들 중 가장 큰 dp값이 3이므로 3+1 =4를 현재 dp값으로 기록

▶ 현재 값은 8이고 8보다 작은 이전 원소들 중 가장 큰 dp값이 3이므로 4+1 =5를 현재 dp값으로 기록

▶ 현재 값은 5이고 5보다 작은 이전 원소들 중 가장 큰 dp값이 3이므로 3+1 =4를 현재 dp값으로 기록
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int arr[] = { 1, 6, 3, 4, 2, 7, 8, 5 };
int dp[] = new int[8];
dp[0] = 1;
for (int i = 1; i < 8; i++) {
int tmp = 1;
for (int j = 0; j < i; j++) {
if(arr[j] < arr[i]) {
tmp = Math.max(tmp, dp[j]);
}
dp[i] = tmp+1;
}
}
for (int i = 0; i < 8; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
for (int i = 0; i < 8; i++) {
System.out.print(dp[i]+" ");
}
}
}↓결과
1 6 3 4 2 7 8 5
1 2 2 3 2 4 5 4
2-2. 이분탐색 : 시간 복잡도 O(NlogN)
- 수열 LIS를 만들어 놓고 하나씩 채워나가면서 LIS를 유지하기 위한 최적의 위치에 수를 삽입하는 방식
- 장점 : lower_bound를 이용하여 시간 복잡도 O(NlogN)까지 줄일 수 있음
- 이용 : LIS의 길이를 구할 때 사용

▶ 첫 값은 첫자리에 놓음

▶ 오름차순이므로 다음 순서에 수를 놓음

▶ 이분 탐색으로 처음으로 3보다 커지는 자리에 3을 놓음

▶ 오름차순이므로 다음 순서에 수를 놓음

▶ 이분 탐색으로 처음으로 2보다 커지는 자리에 2를 놓음

▶ 오름차순이므로 다음순서에 수를 놓음

▶ 오름차순이므로 다음순서에 수를 놓음

▶ 이분 탐색으로 처음으로 5보다 커지는 자리에 5를 놓음
import java.util.*;
public class Main {
public static int lowerBound(int[] array, int value, int s, int e) {
while (s < e) {
int mid = s + (e - s)/2;
if (value <= array[mid]) {
e = mid;
} else {
s = mid + 1;
}
}
return s;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int arr[] = { 1, 6, 3, 4, 2, 7, 8, 5 };
int LIS[] = new int[8];
int cnt = 0;
LIS[cnt++] = arr[0];
for (int i = 1; i < 8; i++) {
if(LIS[cnt-1] < arr[i]) {
LIS[cnt++] = arr[i];
}else {
int idx = lowerBound(LIS, arr[i], 0, cnt);
LIS[idx] = arr[i];
}
}
for (int i = 0; i < 8; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
for (int i = 0; i < 8; i++) {
System.out.print(LIS[i]+" ");
}
}
}↓결과
1 6 3 4 2 7 8 5
1 2 4 5 8 0 0 0
**예제문제
https://cocoon1787.tistory.com/701
[JAVA] 백준 11053번 - 가장 긴 증가하는 부분 수열
📖 문제 📋 코드 import java.util.*; public class Main { public static void main(String[] args){ Scanner sc = new Scanner(System.in); int ans = 0; int n = sc.nextInt(); int arr[] = new int[n]; int..
cocoon1787.tistory.com
https://cocoon1787.tistory.com/702
[JAVA] 백준 11054번 - 가장 긴 바이토닉 부분 수열
📖 문제 📋 코드 import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int ans = 0; int n = sc.nextInt(); int S[] = new int[n]; int up[] = new int[n]; int down[] = new int[n]; for (int
cocoon1787.tistory.com
참고)
[알고리즘]최장 증가 부분 수열 알고리즘(LIS)
원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열을 최장 증가 부분 수열이라고 합니다.예를 들어
velog.io
https://chanhuiseok.github.io/posts/algo-49/
알고리즘 - 최장 증가 부분 수열(LIS) 알고리즘
컴퓨터/IT/알고리즘 정리 블로그
chanhuiseok.github.io
LIS (Longest Increasing Subsequence) - 최장 증가 부분 수열
주어진 수열에서 을 구하는 문제 유형을 알아보자. 사실 이 유형은 DP(Dynamic Programming) 문제로 자주 나오는 유형이며, O(N^2)의 시간복잡도를 갖는 알고리즘과 O(NlogN)의 시간 복잡도를 갖는 알고리
rebro.kr
https://cocoon1787.tistory.com/713
[Algorithm] 최장 증가 부분 수열(LIS) 알고리즘 (JAVA로 구현)
🚀 📖 최장 증가 부분 수열 (Longest Increasing Subsequence)이란? 어떤 수열이 주어질 때 그 수열에서 몇 개의 수들을 제거하여 부분 수열을 만들 수 있는데 그중에서 오름차순으로 정렬된 가장 긴 수
cocoon1787.tistory.com
'CS지식 > 알고리즘' 카테고리의 다른 글
| [CS지식 - 알고리즘] 순열과 조합 (0) | 2023.01.19 |
|---|---|
| [CS 지식 - 알고리즘] 최소공통조상(LCA) (0) | 2023.01.19 |
| [CS 지식 - 알고리즘] 해시테이블(Hash Table) (0) | 2023.01.17 |
| [CS 지식 - 알고리즘] 계수정렬(Counting Sort) (0) | 2023.01.16 |
| [CS 지식 - 알고리즘] 기수정렬(Radix Sort) (0) | 2023.01.16 |



